品质因数Q,也被称品质因素,表征一个储能器件(如电感线圈、电容等)、谐振电路所储能量同每周损耗能量之比的一种质量指标,元件的Q值愈大,用该元件组成的电路或网络的选择性愈佳。
品质因数Q是一种将总存储能量与耗散能量(损耗)相关联的属性-
\begin{align} \label{eq:13601a}
Q = 2\pi \left[ \frac{\textsf{总存储能量}}{\textsf{每循环消耗的能量}} \right]
\end{align}
“每个周期耗散的能量”是维持固定量的振动所需的外部能量(功)。如果分子和分母乘以频率f(周期/秒),分母变成“能量耗散/秒”(即功率),因此上述方程也可以写成- Q没有单位
\begin{align} \label{eq:13602a}
Q = 2\pi \, f \left[ \frac{\textsf{总存储能量}}{\textsf{功率}} \right]
\end{align}
可以为任何系统(电气,机械等)或系统的任何单个组件或部分确定Q。注意,对于“完美”系统(即,没有能量耗散),Q是无限的。
共振系统 #
对于自由振荡的谐振系统,Q表示振荡由于能量损耗而衰减的速率。较高Q值表示衰减相对较慢(图1的示例),而较低Q值表示相对较快的衰减。
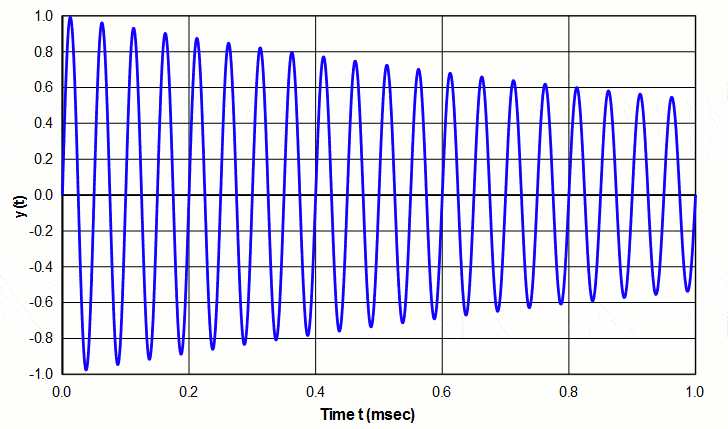
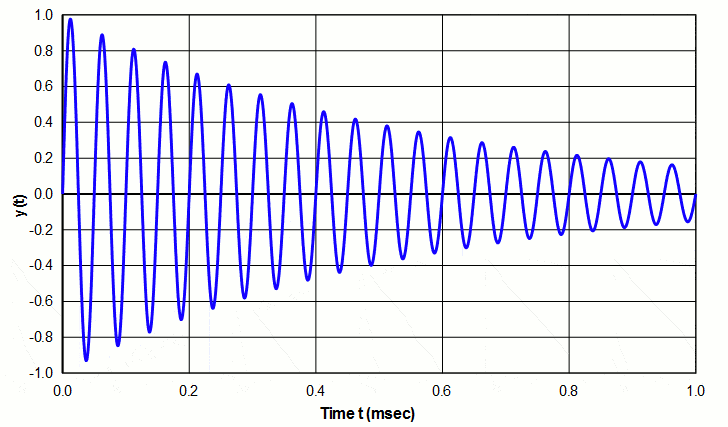
在超声系统中,能量损失可能来自振动材料内部的内部摩擦(随着温度的升高而出现),传递给支撑结构或空气的能量或传递给负载的能量。另外,换能器将由于电流而具有电(电阻)损耗。
非共振系统 #
尽管Q通常用于谐振系统,但这不是必需的。 实际上,等式(1)和(2)可以等效地应用于非谐振系统,尤其是电容器和电感器。
非理想电容器(即损耗电容器)可以表示为与电阻RC串联的理想电容器C。
对于电容器-
\begin{align} \label{eq:13603a}
Q &= \frac{R_C}{(1/2\pi \, f \, C)} \\[0.7em]%eqn_interline_spacing
&= R \, (2\pi \, f \, C) \nonumber
\end{align}
对于电感器-
\begin{align} \label{eq:13604a}
Q &= \frac{R_L}{(2\pi \, f \, L)}
\end{align}
字幕分别代表
RC =电容器的等效电阻
RL =电感的等效电阻
C =电容
L =电感
f =频率
谐振器材料Q值 #
对于用于超声谐振器的材料,相关因素。
Q值是一种材料特性(类似于弹性模量)。但是,必须指定测试条件,因为Q可能取决于:
- 材料的热处理。例如,D2工具钢在硬化后损耗(功率)明显降低,因此Q值更高。
- 零件所受的应变。通常Q值会随着应变的增加而减小,但这取决于材料的特定。
Q值通常与频率无关。
用于压电陶瓷 Q值取决于操作条件(静态压缩,电场,温度等)。
如果已知材料的Q值,则可以根据公式以下确定存储的能量(势能(应变能)或动能),可以计算出谐振器的理论功率—
\begin{align} \label{eq:13605a}
\textsf{Power} = 2\pi \, f \left[ \frac{\textsf{Energy stored}}{Q} \right]
\end{align}
